描述
万字纹”卍”是中国古代传统纹样之一,是古代一种符咒,用做护身符或宗教标志,常被认为是太阳或火的象征。”卍”字在梵文中意为“吉祥之所集”,佛教认为它是释迦牟尼胸部所现的瑞相,有吉祥、万福和万寿之意。用”卍”字四端向外延伸,又可演化成各种锦纹,这种连锁花纹常用来寓意绵长不断和万福万寿不断头之意,也叫”万寿锦”。
国家博物馆正在筹备一个关于万字纹的展览,想请你做一个万字纹的背景图,要求如下:
给定 $N$ 个万字纹,万字纹由中心坐标 $(x,y)$ 和样式 $(p,q)$ 的形式给出。万字纹为中心对称图形,可看作由第二象限中的图案绕中心 $(x,y)$ 分别旋转$90^\circ,180^\circ,270^\circ$拼得,如下图所示:
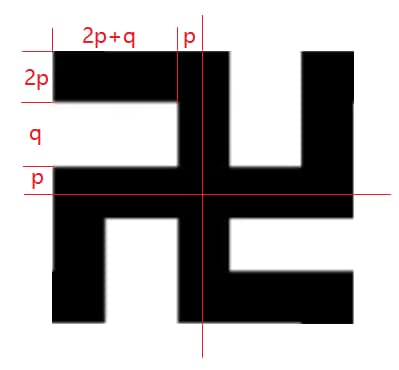
背景图的中心点为原点 $(0,0)$长、宽分别为含万字纹纹样格子横、纵坐标绝对值极值的两倍(参考样例2)。没有纹样的格子用大写字母 $B$ 表示,有单层纹样的格子用 $S$ 表示,有多层纹样的格子用 $M$ 表示。
输入
第一行一个整数 $N,N\le10^4$
随后的 $N$ 行,每行四个正整数 $x,y,p,q, |x|,|y|\le10^5,1\leq p,q \le6$
保证输出的图形的面积 $S\le5\times 10^5$
输出
第一行输出矩阵的长和高,中间用空格隔开;
从第二行开始输出一个大写字母矩阵表示背景图;
另起一行两个整数,中间用空格隔开,表示单层纹样的格子和多层纹样的格子各有多少。
输入样例 1
输出样例 1
12 12
BBSSSSSSBBSS
BBSSSSSSBBSS
SSSSSSSSSSSS
SSSSSSSSSSSS
BBSSMMSSMMSS
BBSSMMSSMMSS
SSMMSSMMSSBB
SSMMSSMMSSBB
SSSSSSSSSSSS
SSSSSSSSSSSS
SSBBSSSSSSBB
SSBBSSSSSSBB
104 16
|
输入样例 2
输出样例 2
10 12
BBSSSSSBSS
BBSSSSSBSS
BBBBBSSBSS
BBSSSSSSSS
BBSSSSSSSS
BBSSBSSBBB
BBSSBSSSSS
BBSSBSSSSS
BBBBBBBBBB
BBBBBBBBBB
BBBBBBBBBB
BBBBBBBBBB
52 0
|
提示
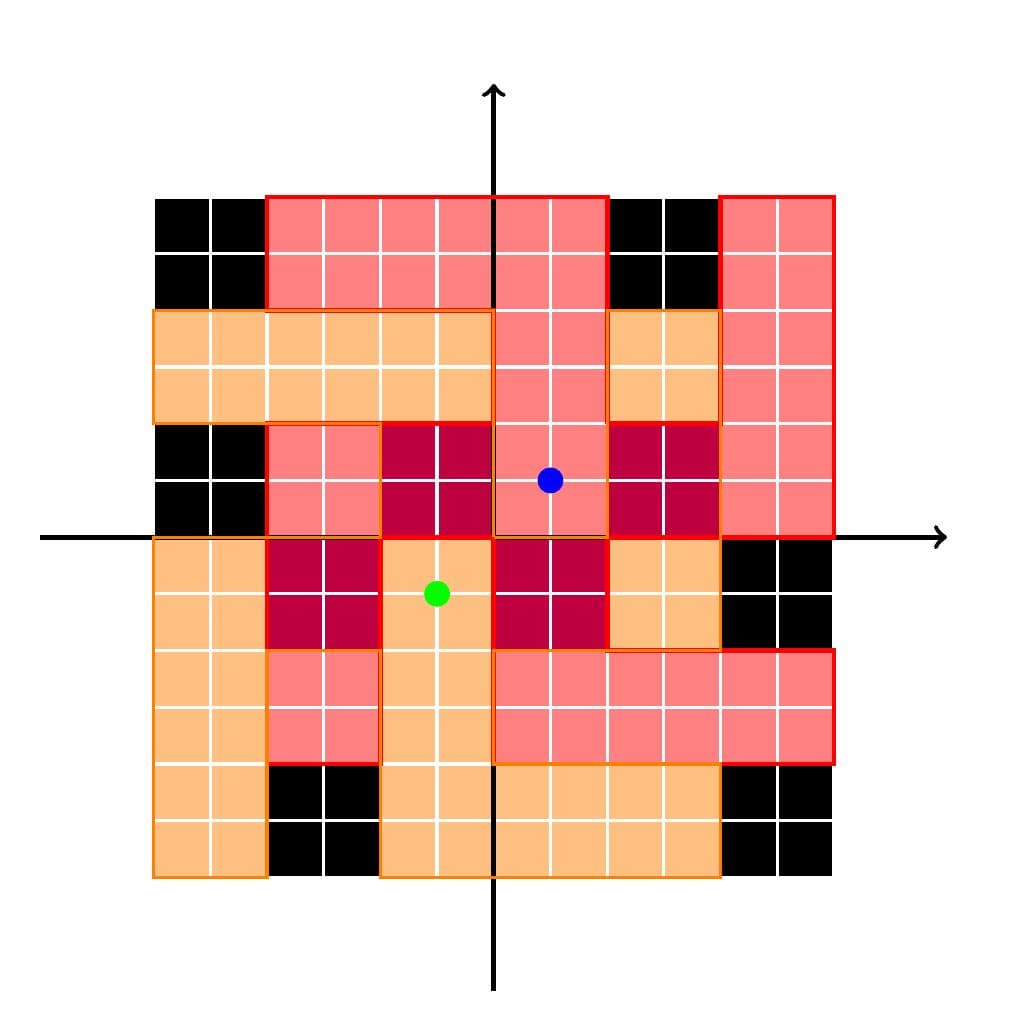
样例1解释:
如图所示,以蓝色圆点 $(1,1)$ 的万字纹与以绿色圆点 $(-1,-1)$
解法
#include <bits/stdc++.h>
int S = 0;
int M = 0;
std::vector<std::vector<char>> array;
void checkAndChange(int x, int y) {
if (array[x][y] == 'B') {
array[x][y] = 'S';
S++;
} else if (array[x][y] == 'S') {
array[x][y] = 'M';
S--;
M++;
}
}
int main() {
int n;
std::cin >> n;
int x[10005], y[10005], p[10005], q[10005];
int width = 0, height = 0;
for (int i = 0; i < n; ++i) {
std::cin >> x[i] >> y[i] >> p[i] >> q[i];
if (abs(x[i] - (3 * p[i] + q[i])) * 2 > width) {
width = abs(x[i] - (3 * p[i] + q[i])) * 2;
}
if (abs(x[i] + (3 * p[i] + q[i])) * 2 > width) {
width = abs(x[i] + (3 * p[i] + q[i])) * 2;
}
if (abs(y[i] - (3 * p[i] + q[i])) * 2 > height) {
height = abs(y[i] - (3 * p[i] + q[i])) * 2;
}
if (abs(y[i] + (3 * p[i] + q[i])) * 2 > height) {
height = abs(y[i] + (3 * p[i] + q[i])) * 2;
}
}
std::cout << width << " " << height << std::endl;
array.resize(width);
std::fill(array.begin(), array.end(), std::vector<char>(height, 'B'));
float x0 = (width / 2) - 1 + 0.5, y0 = (height / 2) - 1 + 0.5;
for (int i = 0; i < n; ++i) {
float centerx = x0 + x[i], centery = y0 - y[i];
for (int j = 1; j <= p[i]; ++j) {
for (int k = 1; k <= p[i]; ++k) {
checkAndChange((int) (centerx + j - 0.5), (int) (centery - k + 0.5));
checkAndChange((int) (centerx + j - 0.5), (int) (centery + k));
checkAndChange((int) (centerx - j + 0.5), (int) (centery - k + 0.5));
checkAndChange((int) (centerx - j + 0.5), (int) (centery + k));
}
}
for (int j = 1; j <= p[i]; ++j) {
for (int k = 1; k <= 2 * p[i] + q[i]; ++k) {
checkAndChange((int) (centerx + j - 0.5), (int) (centery - p[i] - k + 0.5));
checkAndChange((int) (centerx + j - 0.5), (int) (centery + p[i] + k));
checkAndChange((int) (centerx - j + 0.5), (int) (centery - p[i] - k + 0.5));
checkAndChange((int) (centerx - j + 0.5), (int) (centery + p[i] + k));
}
}
for (int j = 1; j <= 2 * p[i] + q[i]; ++j) {
for (int k = 1; k <= p[i]; ++k) {
checkAndChange((int) (centerx + p[i] + j - 0.5), (int) (centery - k + 0.5));
checkAndChange((int) (centerx + p[i] + j - 0.5), (int) (centery + k));
checkAndChange((int) (centerx - p[i] - j + 0.5), (int) (centery - k + 0.5));
checkAndChange((int) (centerx - p[i] - j + 0.5), (int) (centery + k));
}
}
for (int j = 1; j <= 2 * p[i]; ++j) {
for (int k = 1; k <= 2 * p[i] + q[i]; ++k) {
checkAndChange((int) (centerx + p[i] + q[i] + j - 0.5), (int) (centery - p[i] - k + 0.5));
checkAndChange((int) (centerx - p[i] - q[i] - j + 0.5), (int) (centery + p[i] + k));
}
}
for (int j = 1; j <= 2 * p[i] + q[i]; ++j) {
for (int k = 1; k <= 2 * p[i]; ++k) {
checkAndChange((int) (centerx + p[i] + j - 0.5), (int) (centery + p[i] + q[i] + k));
checkAndChange((int) (centerx - p[i] - j + 0.5), (int) (centery - p[i] - q[i] - k + 0.5));
}
}
}
for (int i = 0; i < height; ++i) {
for (int j = 0; j < width; ++j) {
std::cout << array.at(j).at(i);
}
std::cout << std::endl;
}
std::cout << S << " " << M;
return 0;
}
|










